- What is a Data Structure & Types of Data Structures
- What is an Algorithm & It's Characteristics
- Asymptotic Notations
- What is Space Complexity
- Array in Data Structure
- Algorithm for Insertion in Array
- Sparse Matrix
- Introduction to a Linked List
- Algorithm to Insert a Node at the End of the Linked list
- Algorithm to Insert a Node at the Front of the Linked List
- Algorithm to Delete a Node from Linked list
- Circular Linked List
- Algorithm to Insert a Node in the Circular Linked list
- Algorithm to Delete a Node from the Circular Linked list
- Doubly Linked List
- Algorithm to Insert a Node at the End of the Doubly Linked list
- Algorithm to Delete a Node from the Doubly Linked List
- Stack Data Structure
- Algorithm to convert Infix to Postfix
- Queue Data Structure
- Circular Queue in Data Structure
Array in Data Structure
Arrays
An array is a linear data structure that collects elements of the same data type and stores them in a contiguous memory location. This
makes it easier to calculate the position of each element by simply adding an
offset to a base value, i.e., the memory location of the first element of the
array.
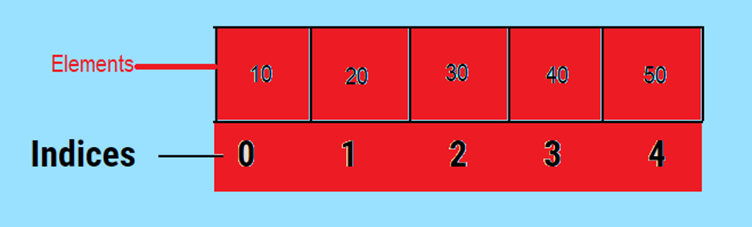
Properties of Array
There are some of the properties of an that are
listed as follows -
- ·
Each
element in an array is of the same data type and carries the same size.
- ·
Elements
in the array are stored at contiguous memory locations, and the first element
is stored at the smallest memory location.
- ·
Elements
of the array can be randomly accessed since we can calculate the address of
each element of the array with the given base address and the data element's
size.
- ·
Arrays
are best for storing multiple values in a single variable
Why Do
You Need an Array in Data Structures?
Consider a class of 20 students
that is required to submit its results. It would be difficult to manipulate and
maintain the data if you had declared each of the 20 variables separately.
It would be more challenging to
declare and maintain track of all the variables if more students joined. Arrays
were introduced as a solution to this issue.
Types
of arrays
1.
Single Dimensional
A single-dimensional
Array is the simplest form of an Array data structure in which the
elements are stored linearly and can be accessed individually by specifying the
index value of each element stored in the array.
Declaration
Syntax
data_type
array_name [array_size] ;
Example:
int x[10];
2.
Multidimensional
A multi-dimensional array can be termed as an array of arrays
that stores similar data in tabular form. Data in multidimensional arrays can
be stored in row-major order and Column major order.
Declaration
Syntax
data_type
array_name [number of rows][number of columns] ;
Example: int x[4][4];
Here, x is a two-dimensional array. The array can
hold 16 elements. You can think of the array as a table with 4 rows and each
row has 4 columns.
1
2 3
4
A11
A12
A13
A14
A21
A22
A23
A24
A31
A32
A33
A34
A41
A42
A43
A44
Similarly,
you can declare a three-dimensional array.
Declaration
Syntax
data_type
array_name [blocks size][number of rows][number of columns] ;
Example:
int x[3][4][3];
Here, the array x can hold 36 elements.
Row Major
Order
RMO:
Loc(a[i][j])= B.A. + w [(i-lb1)* nc + (j-lb2)]
A11
A12
A13
A14
A21
A22
A23
A24
A31
A32
A33
A34
A41
A42
A43
A44
Column
Major Order
CMO:
Loc(a[i][j])= B.A. + w [(j-lb2)* nr + (i-lb1)]
A11
A21
A31
A41
A12
A22
A32
A42
A13
A23
A33
A34
A14
A24
A34
A44
Example: Let A be a two-dimensional
array declared as follows:
A: array
[1 …. 10] [1 ….. 15] of integer;
Assuming
that each integer takes one memory location, the array is stored in row-major
order and the first element of the array is stored at location 100, what
is the address of the element A[i][j]? (GATE-1998)
Solution:
Number of column= (upper bound2 - lower bound2) + 1=
15-1+1=15
Base address: 100
w=1
Loc(A[i][j])= B.A. + w [(i-lb1)* nc + (j-lb2)]
Loc(A[i][j])=100+1[(i-1)*15+(j-1)]
Loc(A[i][j])=100+15i-15+j-1
Loc(A[i][j])=15i+j+84
Basic
operations
- Traversal - This
operation is used to print the elements of the array.
- Insertion - It is used
to add an element to a particular index.
- Deletion - It is used
to delete an element from a particular index.
- Search - It is used
to search an element using the given index or by the value.
- Update - It updates
an element at a particular index.
Complexity
of Array operations
Time
Complexity
Operation
Average Case
Worst Case
Access
O(1)
O(1)
Search
O(n)
O(n)
Insertion
O(n)
O(n)
Deletion
O(n)
O(n)
Space Complexity
In
array, space complexity for the worst case is O(n).
Advantages
of Array
- ·
Array
provides a single name for the group of variables of the same type. Therefore,
it is easy to remember the names of all the elements of an array.
- ·
You can
randomly access elements in the array using an index number.
- ·
Traversing
an array is a very simple process; we just need to increment the base address
of the array to visit each element one by one.
- ·
2D arrays
can efficiently represent the tabular data.
Disadvantages
of Array
- ·
Array
is homogenous. It means that the elements with similar data types can be stored
in it.
- ·
In
an array, there is static memory allocation that the size of an array cannot be
altered.
- ·
There
will be a waste of memory if we store less number of elements than the declared
size.
- ·
Insertion
and deletion operation in an array is quite tricky as the array stores elements
in continuous form.
Applications of
Arrays
- ·
They are cache-friendly.
- ·
Storing
data in a tabular format
- ·
Online
ticket booking system-Multidimensional array
- ·
Storing a
list of data elements belonging to the same data type
- ·
Storage
of binary tree elements of fixed count