Algorithm for Insertion in Array

Algorithm
for inserting elements into an array:

Insert(array, N, K, Element)

N=No. of elements

K= Position 

1. [Initialize counter] Set J:=N

2. Repeat steps 3 and 4 while (J>=K)

3. [Move Jth element downward] Set array[J+1]=
array[J]

4. [Decrease counter] Set J:=J-1

     [End of
step 2 loop]

5. [Insert element] Set array[K]:= element

6. [Reset N] Set N:=N+1

7. Exit 

 

Visual Representation

Let's
take an array of 5 integers.

11, 12,
5, 90, 20.

If we
need to insert an element 80 at position 2, the execution will be,

 



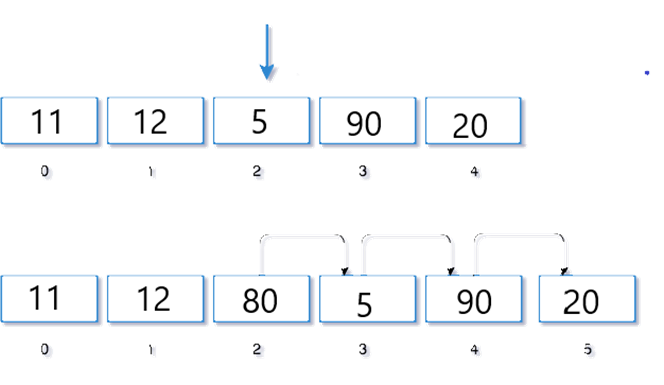
Algorithm
for deleting an element from an array:

Algorithm for deleting elements into an array:

Delete (array, N, K, element)

N=No. of elements

K= Position 

 

1. [Initialize counter] Set J:=K

2. Repeat steps 3 and 4 while (J<N)

3. [Move Jth element backward (left)] Set array[J]=
array[J+1]

4. [Increase counter] Set J:=J+1

5. [Decrement counter] Set N:=N-1

     [End of
step 2 loop]

5. [Reset N] Set N:=N-1

6. Exit 


Visual
Representation

Let's
take an array of 5 elements.

11, 12,
5, 90, 20.

If we
remove element 12 from the array, the execution will be,

 


 


The
time complexity to insert and remove an element from the array is O(n) in the worst
case.